 |
Old Bull Lee A Voice From the Reality-based Community Notes from a Study of Things Themselves |
 |
A Hundred Wins and No Losses with Windows 7 Solitaire - How To Do It
The MS Windows 7 Solitaire game maintains a cumulative record of games played and games won since the most recent reset of the counters. Since a large percentage of games cannot be won no matter how they are played, it would seem to be nearly impossible to build a long winning streak. For example, if we assume 50% of deals can be won, then, at best, the odds of winning 100 straight games would be one in 2100, an astronomical number.
However, the screen-capture below shows that a record of a hundred consecutive wins can be achieved, at least on my desktop HP PC.
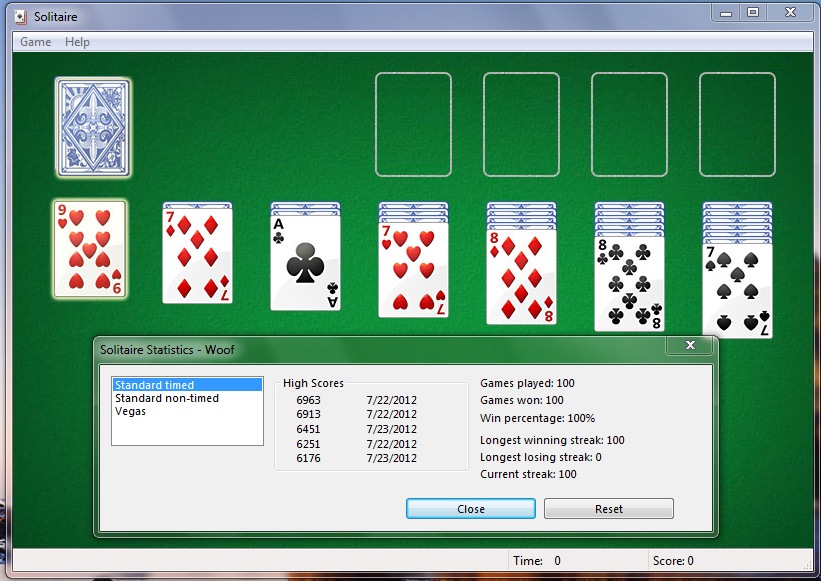
A Technique For Building an Unbroken Series of Wins
The technique for winning consecutive games exploits three observations about the Solitaire software as implemented in Windows 7 Home Premium, Version 6.1 (Build 7601; Service Pack 1). The "draw three" mode is used and standard scoring is assumed.
Observation #1. If two hands show the same sequence of face-up cards after the deal, then both hands will play out the same way. In other words, a deal sets the sequence of all 52 cards at once, including the 45 cards not shown face-up. Most importantly, if we know that a hand dealt with a particular sequence of face-up cards was won once, then it can be won whenever the same sequence appears in any future deal.
Observation #2. The set of distinct face-up card sequences that appear immediately after a restart of the Solitaire game is rather small, on the order of a thousand, with some hands appearing much more frequently than others.
Observation #3. A player can exit a game without being assigned a win or loss after viewing the seven face-up cards immediately after the deal and before playing any cards from the deal.
These observations suggest a two-step process for building a record of many consecutive wins.
Step One. Build up a list of at least ten face-up card sequences that can be won after a fresh start of the game. The card sequences that worked for me are shown in the table below. Note that the card sequence shown in the image above is on the winnable list. (The numbers in the rightmost column indicate the times these sequences appeared when I attempted to win 100 consecutive games.)
| 2♣ | 8♦ | A♦ | 6♥ | 3♣ | 2♦ | Q♠ | 15 |
| 2♥ | 3♦ | 8♦ | J♥ | 2♠ | 10♠ | A♥ | 2 |
| 2♠ | 3♥ | 8♣ | K♥ | 4♠ | A♠ | 7♠ | |
| 4♣ | 10♣ | J♦ | 9♥ | 8♣ | 2♦ | J♠ | |
| 4♦ | 3♥ | 10♦ | 7♣ | J♣ | A♥ | 9♦ | 2 |
| 5♣ | 2♣ | Q♦ | A♥ | 7♥ | 8♠ | 3♠ | |
| 5♦ | 4♠ | 4♦ | Q♥ | K♣ | 6♥ | 2♥ | 15 |
| 5♥ | A♥ | A♠ | 9♣ | A♣ | 7♣ | 3♦ | |
| 7♦ | 2♠ | J♥ | 10♣ | 3♠ | 8♣ | 2♦ | 19 |
| 8♠ | A♦ | 7♥ | 9♠ | Q♥ | 10♥ | 10♣ | |
| 9♥ | 7♦ | A♣ | 7♥ | 8♦ | 8♣ | 7♠ | 15 |
| 9♥ | 7♥ | 6♣ | A♥ | 5♣ | J♥ | 4♥ | 1 |
| 10♣ | 10♠ | Q♦ | 9♥ | K♣ | 4♠ | A♣ | |
| J♦ | 7♠ | 2♦ | Q♦ | 7♦ | A♦ | Q♣ | 8 |
| K♣ | 5♦ | 10♥ | 6♥ | 9♦ | 10♣ | J♥ | |
| K♠ | A♦ | 3♣ | 6♦ | K♥ | 6♣ | A♣ | |
| A♦ | 5♠ | 4♦ | 7♠ | 4♥ | A♠ | K♣ | |
| A♥ | 10♣ | 5♠ | 7♣ | K♥ | 6♥ | 2♣ | |
| A♠ | 5♠ | 10♣ | 9♠ | K♥ | A♣ | 3♣ | 8 |
| A♠ | K♠ | J♣ | 5♥ | 9♠ | 8♣ | Q♥ | 15 |
Hints on how to minimize the pain of doing this.
1. Learn the playing techniques that maximize your chances of winning.
2. Don't bother playing hands that look unpromising. For example, exit out of hands where fewer than two cards can be immediately uncovered from the stacks.
3. Write down each unique seven-card sequence you play. Do this immediately after it's dealt. After playing the hand, note whether you won or not.
4. After you finish playing each hand, quit the Solitaire program by clicking on "Exit". Never click on "Play Again".
5. Don't bother playing hands you've already played.
Step Two. Build up your record of N consecutive wins.
1. Reset the Solitaire counters to zero and exit the Solitaire program.
2. Deal a fresh hand by starting the Solitaire program.
3. If the sequence of seven face-up cards is on your list, then play the hand. Otherwise, exit the Solitaire program and go back to Step 2.
4. If you know the hand is winnable, but you get to a dead end, then undo your moves using CNTL-Z. Retry alternate plays until you win.
5. Once you win a hand, click on "Exit" to quit the Solitaire program. Never click on "Play Again." Stop playing if you have reached the desired number of wins. Otherwise, go back to Step 2.
Conjectures As To Why the Technique Works (for Me, At Least)
The Windows 7 Solitaire algorithm must employ some sort of random number generator in dealing cards. A random number generator[1] is a software subroutine that returns a number between 0 and 1 each time it's called. A series of calls to the RNG will generate a series of numbers that have a roughly uniform distribution over the interval [0,1]. The number returned by the RNG can be translated into a number between 1 and 52 that corresponds to a card in the deck.
One way to deal a fresh deck of cards is to call the RNG 52 times. For each call, multiply the the random number by 52 and pick the closest undealt card as the next card to deal.
One quirk of RNGs is that the number sequence they generate eventually repeats. This quirk presents a problem to Solitaire: how does the Solitare algorithm prevent the same hands from being dealt each time the program is started? The answer is to pass the RNG a parameter known as the "seed." If the RNG begins repeating after a million calls, then the seed can be any integer less than a million. So Solitaire program must create a new seed each time it starts. In other words, it must come up with a random number on its own to get the RNG started! (Low-order bits of the computer's internal clock are sometimes used as a seed for an RNG.)
This backgrounder on RNGs leads us to Conjecture #1: A poorly-chosen RNG seed is used when the Solitaire program is started.
Limited experimentation with other Windows 7 computers suggests that the winnable face-up Solitaire card sequences differ from computer to computer. This leads to Conjecture #2: The Solitaire RNG seed at start-up is created from something that is different on different computers.
Further Research into Windows 7 Solitaire
Wikipedia states that at least 82% of Klondike Solitaire games have a winning solution. I was skeptical, but I replayed many hands I'd previously considered unwinnable. To my surprise, I found that a very high percentage could be won. My expanded list of winnable hands (face-up cards after the deal) is shown below.
| 2♣ | 8♦ | A♦ | 6♥ | 3♣ | 2♦ | Q♠ | |
| 2♥ | 3♦ | 8♦ | J♥ | 2♠ | 10♠ | A♥ | |
| 2♠ | 3♥ | 8♣ | K♥ | 4♠ | A♠ | 7♠ | |
| 3♣ | 6♥ | A♣ | 3♥ | J♦ | 7♥ | 6♠ | |
| 3♦ | A♦ | 7♣ | 10♦ | A♣ | 9♥ | 2♣ | difficult |
| 4♣ | 10♣ | J♦ | 9♥ | 8♣ | 2♦ | J♠ | |
| 4♦ | 3♥ | 10♦ | 7♣ | J♣ | A♥ | 9♦ | |
| 4♠ | 7♥ | 6♣ | 8♣ | 4♥ | Q♠ | K♣ | |
| 5♣ | 2♣ | Q♦ | A♥ | 7♥ | 8♠ | 3♠ | |
| 5♦ | 4♠ | 4♦ | Q♥ | K♣ | 6♥ | 2♥ | |
| 5♥ | A♥ | A♠ | 9♣ | A♣ | 7♣ | 3♦ | |
| 5♠ | 8♠ | 9♥ | 7♦ | 3♣ | 8♦ | 4♣ | |
| 6♣ | 6♥ | Q♦ | 4♣ | K♦ | A♦ | 7♦ | |
| 6♣ | 7♦ | J♦ | 10♠ | 5♥ | 7♣ | 6♥ | difficult; build up club stack to promote 7♣ |
| 6♦ | J♠ | A♥ | 7♠ | 8♦ | 3♦ | J♥ | |
| 6♥ | 4♥ | 10♣ | A♠ | 7♥ | K♠ | 9♥ | difficult |
| 6♥ | 7♦ | 5♦ | 8♠ | ♥ | K♥ | 5♣ | |
| 6♥ | 7♠ | A♠ | 4♥ | 8♦ | 7♥ | 8♠ | |
| 7♦ | 2♠ | J♥ | 10♣ | 3♠ | 8♣ | 2♦ | |
| 8♦ | 2♠ | 10♠ | 6♥ | 9♦ | J♥ | Q♠ | |
| 8♦ | 3♠ | 2♦ | 9♥ | A♥ | 2♣ | J♦ | |
| 8♠ | A♦ | 7♥ | 9♠ | Q♥ | 10♥ | 10♣ | |
| 9♥ | 7♦ | A♣ | 7♥ | 8♦ | 8♣ | 7♠ | |
| 9♥ | 7♥ | 6♣ | A♥ | 5♣ | J♥ | 4♥ | |
| 10♣ | 2♦ | 3♣ | 10♦ | 2♣ | A♥ | 9♦ | |
| 10♣ | 10♠ | Q♦ | 9♥ | K♣ | 4♠ | A♣ | |
| 10♣ | A♦ | 3♣ | J♣ | K♣ | 8♦ | J♦ | |
| 10♦ | 3♦ | 7♦ | 9♥ | J♣ | 8♣ | K♣ | difficult |
| 10♥ | 5♥ | 7♦ | Q♣ | 4♠ | 6♦ | 8♠ | difficult; put J♥ on Q♣ |
| 10♥ | 10♣ | Q♥ | 9♣ | J♦ | Q♣ | A♦ | |
| 10♠ | 6♥ | Q♦ | 6♠ | 3♣ | 9♦ | 4♦ | |
| J♣ | A♦ | 5♥ | 6♠ | J♥ | 10♠ | 10♦ | difficult; put 10♥ on J♣ |
| J♦ | 7♠ | 2♦ | Q♦ | 7♦ | A♦ | Q♣ | |
| J♥ | 8♦ | 8♠ | 9♣ | 7♦ | J♣ | 10♥ | difficult |
| Q♦ | Q♠ | 7♦ | K♣ | 8♣ | 2♠ | 5♦ | difficult |
| Q♠ | 2♦ | 7♦ | 10♦ | 2♣ | 3♠ | K♦ | difficult |
| K♣ | 5♦ | 10♥ | 6♥ | 9♦ | 10♣ | J♥ | |
| K♦ | Q♠ | J♦ | 8♦ | 6♣ | 10♦ | A♣ | |
| K♥ | A♣ | J♥ | 3♠ | 8♠ | A♠ | A♥ | difficult |
| K♥ | A♠ | J♥ | Q♦ | 6♠ | 4♥ | K♣ | |
| K♠ | 3♠ | A♣ | 5♠ | Q♦ | A♦ | 7♥ | |
| A♥ | 7♠ | 6♦ | 3♥ | A♦ | Q♣ | J♥ | difficult |
| A♥ | 8♥ | 9♣ | 8♠ | 10♥ | 5♦ | 4♣ | difficult; put 6♥ on 7♠ |
| A♠ | 5♠ | 10♣ | 9♠ | K♥ | A♣ | 3♣ | |
| A♠ | K♠ | J♣ | 5♥ | 9♠ | 8♣ | Q♥ |
All these deals came from a fresh start of the Windows 7 Solitaire program. Only deals where at least two cards could be immediately uncovered from the stacks were played. In no case was the "play again" option selected at the conclusion of a game. I found about one of every three deals was on the winnable list. There were about 2000 deals in the experiment.
Tips for Winning the Apparently Unwinnable Deals
1. Don't give up when you get this message.
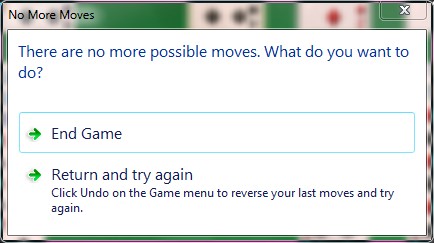
Click on "Return and try again" and back up (use CNTL-Z) to a point in the game where you might play the cards differently, maybe the very beginning.
2. When you reach a dead end or get the "No More Moves" message, make a mental note of the face-up cards on top of stacks of uncovered cards. A card you need to win is likely buried in one of those stacks. So when you replay the deal, make an effort to remove the top card from at least one of those stacks. Your knowledge of card locations gained from earlier play will generally make this possible.
[1] To be precise, we're talking about pseudo-random numbers since a digital computer is 100% deterministic and can not produce a truly random number.